PID控制器
PID控制器是一种常用的反馈控制系统,广泛应用于工业控制系统和各种控制系统中,用来持续调整一个过程的控制输入,以减小系统当前位置和期望位置之间的误差。PID代表比例(Proportional)、积分(Integral)、微分(Derivative)。
控制系统概述
开环控制系统
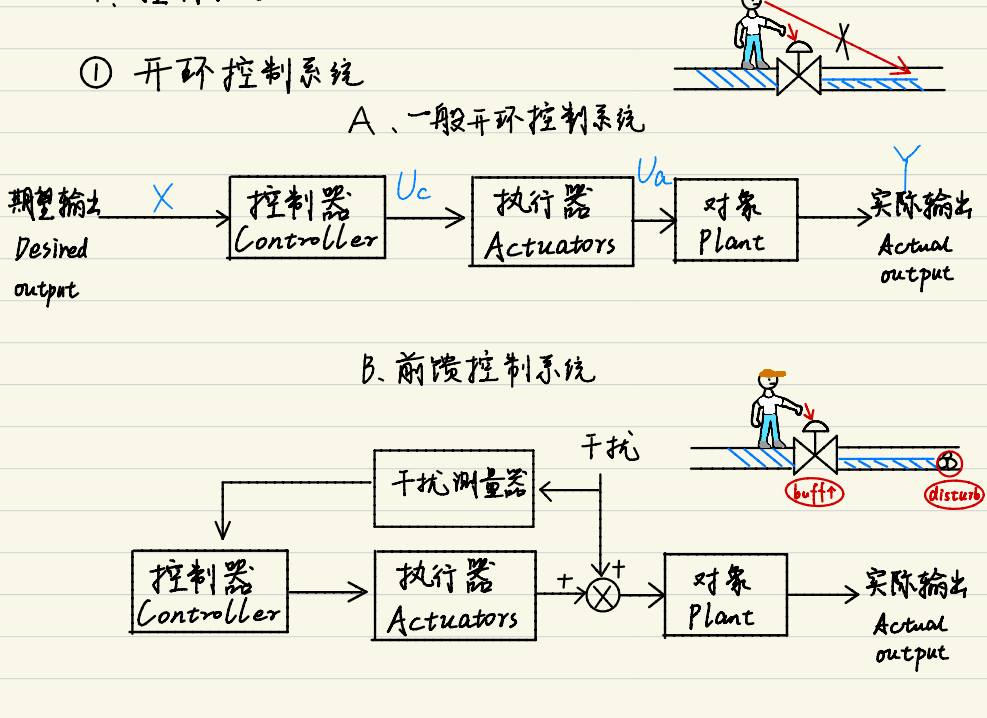
前馈控制系统尝试预先计算扰动对系统的影响,并在扰动影响系统输出之前调整输入以抵消它。
闭环控制系统
控制器接收误差信号。该系统通过反馈回路来自动调节其输出
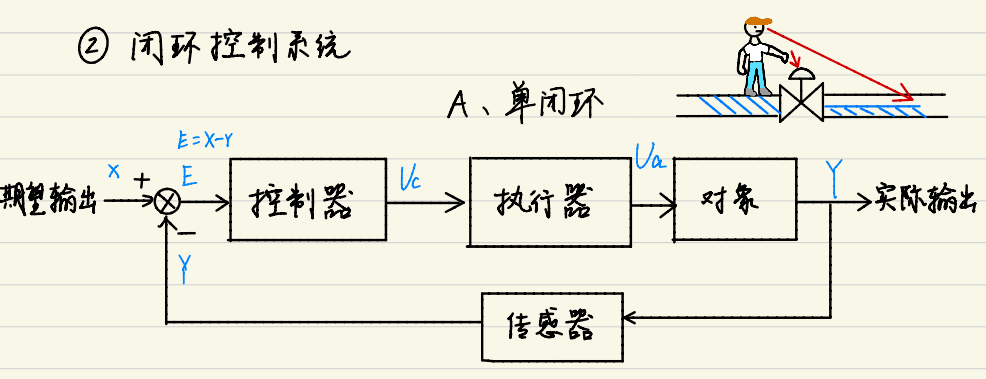
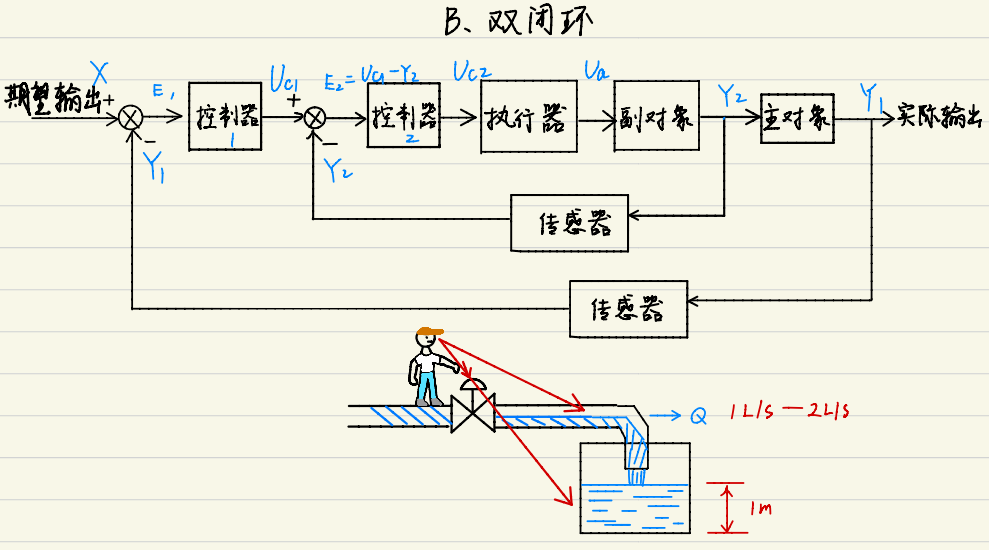
复合控制系统
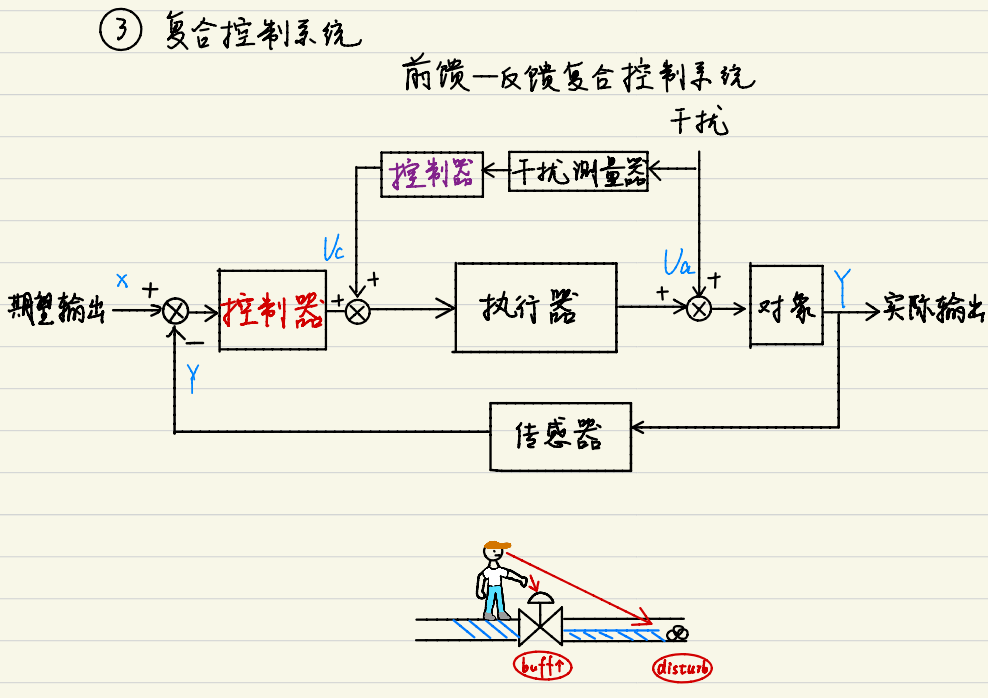
连续与离散信号
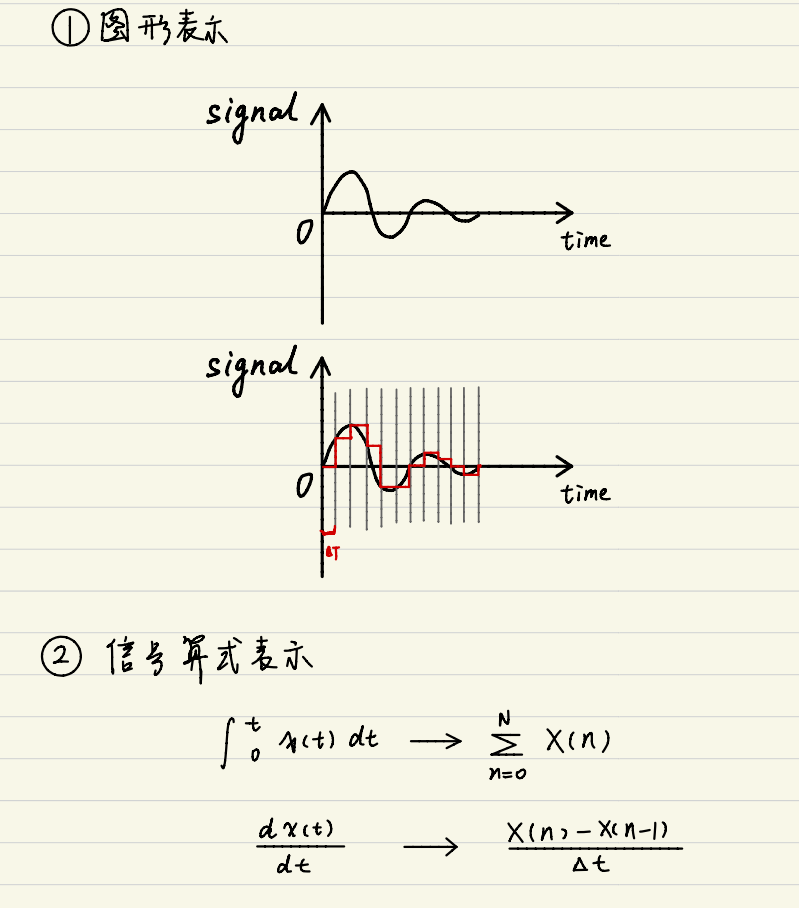
从连续信号到离散信号的转换过程涉及以下步骤:
- 采样:在连续信号上每隔一定时间间隔取一个值。
- 量化:将每个采样值映射到最接近的量化级上。
积分可以通过求和来近似,微分可以通过相邻样本之间的差分来近似。
PID公式
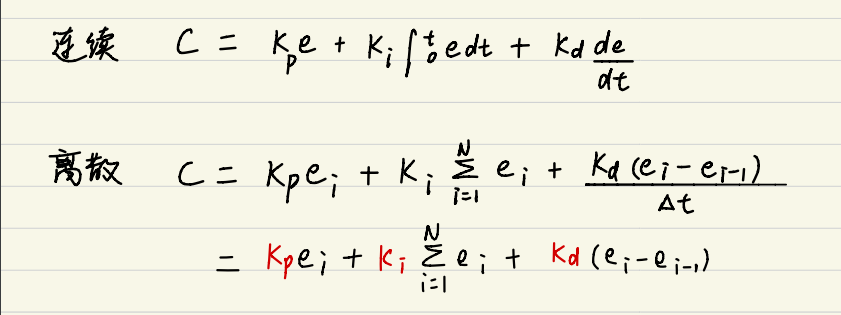
控制系统中的传感器会连续监测被控制对象的状态(例如,温度、压力、位置等),而PID控制器通过在固定的采样间隔收集输入信号,将其转换为离散信号,计算控制动作,然后输出到控制对象。离散PID控制的优势在于其灵活性和适应性,它可以轻松地与软件算法集成。
直观例子
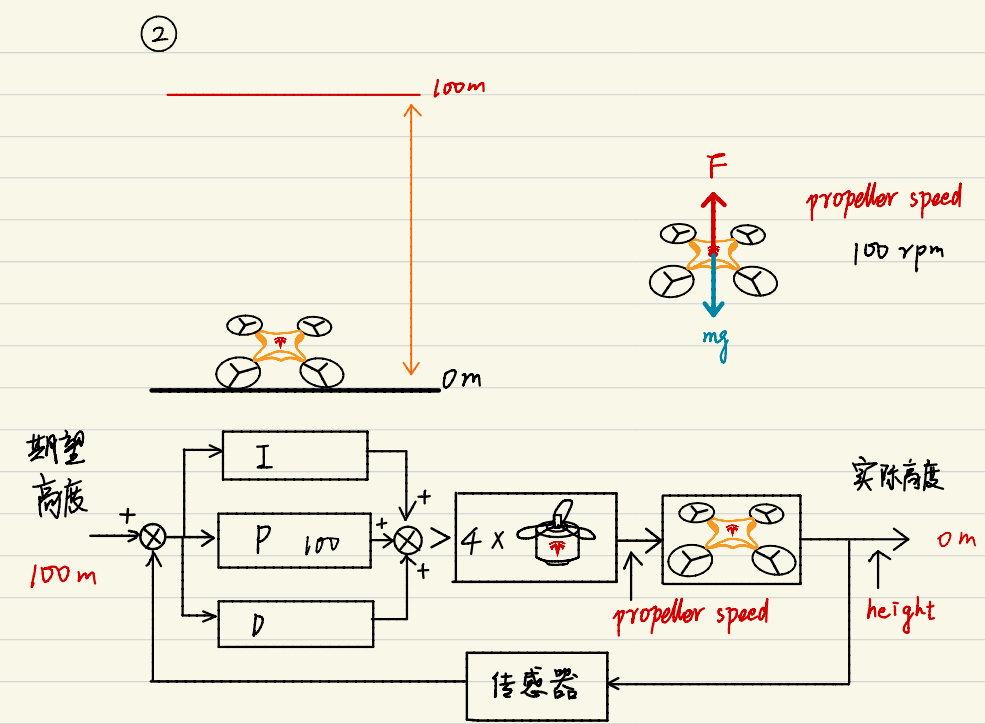

**仅使用比例(P)控制无法消除稳态误差。**稳态误差是指当系统达到平衡状态时,控制系统的实际输出与期望输出之间的差异。
原因:当系统接近其期望点时,误差减小,进而控制器输出也减小。如果控制器输出减小到无法克服系统内部阻力(如摩擦力)或外部扰动的程度时,系统就无法进一步接近设定点,从而留下稳态误差。
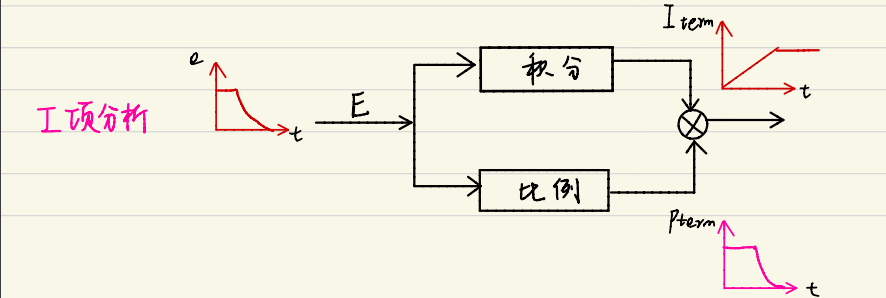
为了解决稳态误差问题,通常会在P控制基础上加入积分(I)控制。积分控制能够累积误差,即使是很小的误差,也会随时间积累,最终产生足够的控制作用以调整系统输出,直到误差为零。
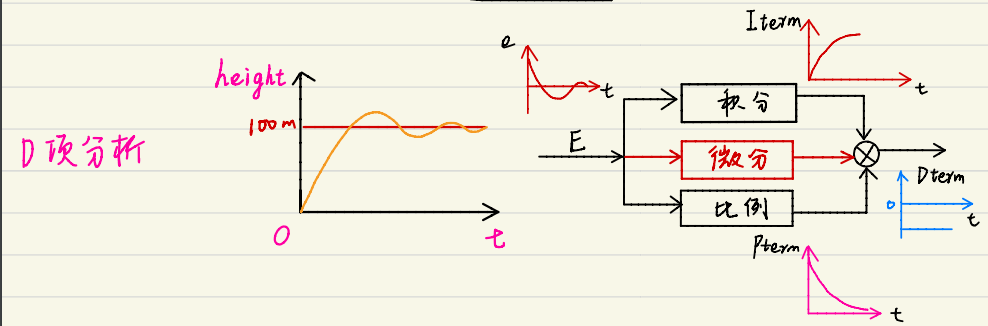
微分控制在PID控制器中的作用主要是提高系统的瞬态响应和稳定性。
$$ {k}_{d}({e}_{i}-{e}_{i-1}) $$ 它通过对误差信号的变化率(即误差的微分)进行响应,来预测系统未来的行为。如果误差在快速变化,微分项会产生一个相对较大的控制作用来尝试减缓这种变化。相关控制知识
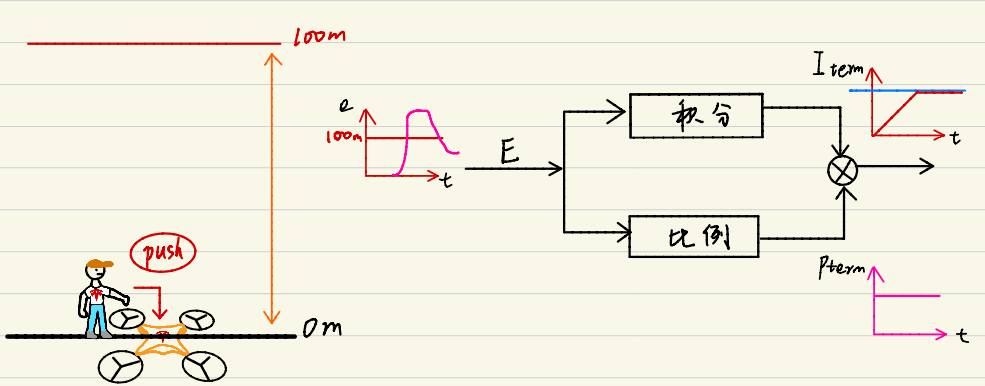
当系统启动时或者遇到大的扰动,会产生大的初始误差。若系统调整缓慢,积分项会在达到目标状态之前累积很大的值。这可导致控制器输出超出了实际的执行器(比如电机、阀门等)可以处理的范围。当这种情况发生时,即使误差减少,由于积分项累积的值太大,控制器的输出可能仍然处于饱和状态。
积分限幅
积分限幅可防止积分项超过预设的上限和下限。
$$ {I}_{clamped}(t)=clamp({I}_{updated(t)},{I}_{max},{I}_{min}) $$积分分离
当误差超过某个预定阈值时,禁用积分作用,仅使用比例(P)和微分(D)控制来快速减小误差,避免因积分作用导致的控制器输出过度响应。
if (abs(error) > threshold) {
// 积分作用被分离,即暂时禁用积分作用
integral = 0;
} else {
// 正常积分累积
integral += error * dt;
}
PID控制器:
def update(self, current_value):
error = self.set_point - current_value
# 实现积分分离逻辑
if abs(error) < self.error_threshold:
self.integral += error * self.dt
# 应用积分限幅
self.integral = max(min(self.integral, self.integral_limit), -self.integral_limit)
else:
# 误差过大时重置积分累积
self.integral = 0
derivative = (error - self.prev_error) / self.dt
# PID 输出
output = self.Kp * error + self.Ki * self.integral + self.Kd * derivative
self.prev_error = error
return output
