KAN
Kolmogorov-Arnold表示定理
该定理表明,任何多元连续函数都可以表示为有限个单变量函数的组合。
对于任意一个定义在$[0,1]^n$上的连续多元函数:
$$ f(x_1, x_2, \ldots, x_n), $$ 存在**单变量连续函数** $\phi_{q}$ 和 $\psi_{q,p}$(其中 $q = 1, 2, \ldots, 2n+1$,$p = 1, 2, \ldots, n$),使得: $$ f(x_1, \ldots, x_n) = \sum_{q=1}^{2n+1} \phi_{q}\left( \sum_{p=1}^{n} \psi_{q,p}(x_p) \right). $$ 即,$f$可以表示为$2n+1$个“外层函数”$\phi_{q}$和$n \times (2n+1)$个“内层函数”$\psi_{q,p}$的组合。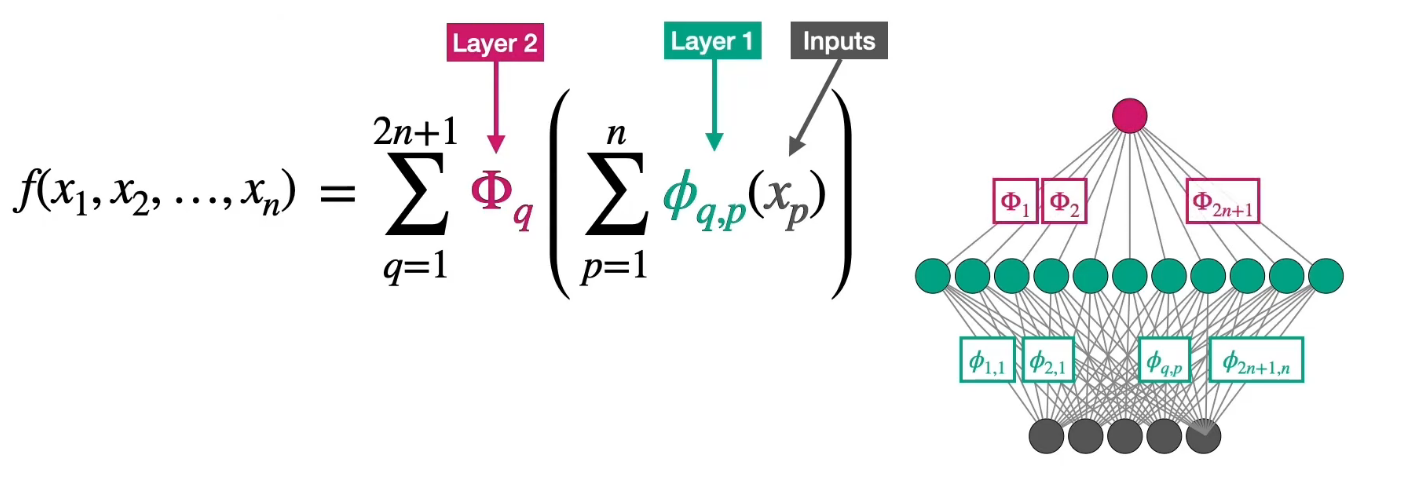
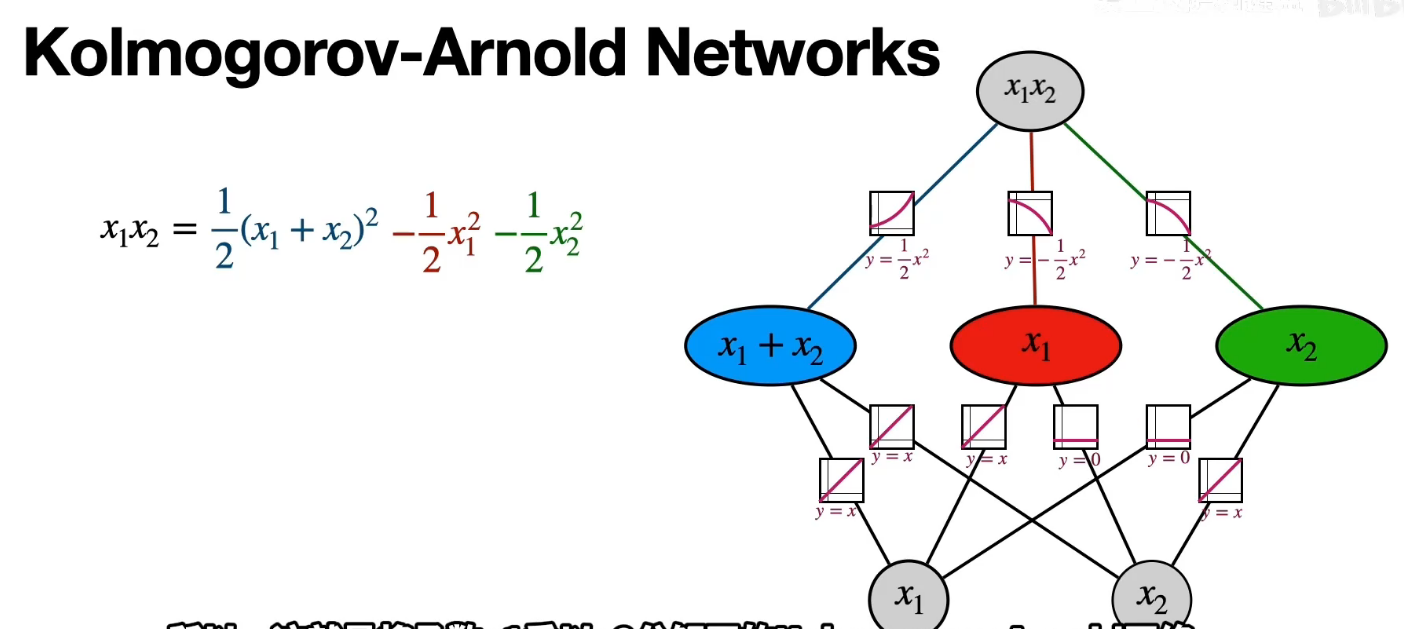
和MLP的联系
| Kolmogorov-Arnold定理 | 神经网络(MLP) |
|---|---|
| 外层函数 $\phi_q$ 的叠加 | 输出层的加权求和(线性组合) + 激活函数 |
| 内层函数 $\psi_{q,p}$ 的线性组合 | 隐藏层的加权求和 + 非线性激活函数 |
| 固定 $2n+1$ 个“隐藏单元” | 隐藏层神经元数量可以自由设计,依赖于网络的深度和宽度 |
| 严格的数学构造(存在性证明) | 通过数据驱动的学习(基于梯度下降等方法)来优化参数 |
和MLP的差异
浅层结构(一个隐藏层)的数学表达与模型设计
| 模型 | 数学公式 | 模型设计 |
|---|---|---|
| MLP | $f(x) \approx \sum_{i=1}^{N} a_i \sigma(w_i \cdot x + b_i)$ | 线性变换后再跟非线性激活函数(RELU) |
| KAN | $f(x) = \sum_{q=1}^{2n+1} \Phi_q \left( \sum_{p=1}^n \phi_{q,p}(x_p) \right)$ | 可学习激活函数(如样条)在边上,求和操作在神经元上 |
边上的可学习函数: $\phi_{q,p}(x_p)$(如B样条)
求和操作:$\sum_{p=1}^n \phi_{q,p}(x_p)$

深层结构的数学表达与模型设计
| 模型 | 数学公式 | 模型设计 |
|---|---|---|
| MLP | $\text{MLP}(x) = (W_3 \circ \sigma_2 \circ W_2 \circ \sigma_1 \circ W_1)(x)$ | 交替的线性层($W_i$)和固定非线性激活函数($\sigma_i$)。 |
| KAN | $\text{KAN}(x) = (\Phi_3 \circ \Phi_2 \circ \Phi_1)(x)$ | 每一层都是单变量函数的组合($\Phi_i$),每一层的激活函数都可以进行学习 |
传统MLP的缺陷
- 梯度消失和梯度爆炸: 与其他传统的激活函数(如 Sigmoid 或 Tanh)一样,MLP 在进行反向传播时有时就会遇到梯度消失/爆炸的问题,尤其当网络层数过深时。当它非常小或为负大,网络会退化;连续乘积会使得梯度慢慢变为 0(梯度消失)或变得异常大(梯度爆炸),从而阻碍学习过程。
- 参数效率: MLP 常使用全连接层,每层的每个神经元都与上一层的所有神经元相连。尤其是对于大规模输入来说,这不仅增加了计算和存储开销,也增加了过拟合的风险。效率不高也不够灵活。
- 处理高维数据能力有限:MLP 没有利用数据的内在结构(例如图像中的局部空间相关性或文本数据的语义信息)。例如,在图像处理中,MLP 无法有效地利用像素之间的局部空间联系,这很典型在图像识别等任务上的性能不如卷积神经网络(CNN)。
- 长依赖问题: 虽然 MLP 理论上可以逼近任何函数,但在实际应用中,它们很难捕捉到序列中的长依赖关系(例如句子跨度很长)。这让人困惑:如何把前后序列的信息互相处理?而自注意力(如 transformer)在这类任务中表现更好。
但无论CNN/RNN/transformer怎么改进,都躲不掉MLP这个基础模型根上的硬伤,即线性组合+激活函数的模式。
KAN网络
主要贡献:
过去的类似想法受限于原始的Kolmogorov-Arnold表示定理(两层网络,宽度为2n+12n+1),未能利用现代技术(如反向传播)进行训练。
KAN通过推广到任意宽度和深度的架构,解决了这一限制,同时通过实验验证了KAN在“AI + 科学”任务中的有效性,兼具高精度和可解释性。
B样条(B-spline)
是一种通过分段多项式函数的线性组合构造的光滑曲线,其核心思想是利用局部基函数(称为B样条基函数)来表示整个曲线。
形式上,一个B样条函数通常表示为基函数的线性组合:
$$ S(t) = \sum_{i=0}^{n} c_i \cdot B_i(t) $$其中:
- $B_i(t)$ 是 B样条基函数(basis functions);
- $c_i$ 是 控制点 或系数(可以来自数据、拟合、插值等);
- $S(t)$ 是最终的 B样条曲线 或函数。
每个基函数只在某个局部区间内非零,改变一个控制点只会影响曲线的局部形状。
示例:基函数定义
$B_0(t)$ - 支撑区间[0,1]
$$ B_0(t) = \begin{cases} 1 - t, & 0 \leq t < 1,\\ 0, & \text{其他区间}. \end{cases} $$$B_1(t)$ - 支撑区间[0,2]
$$ B_1(t) = \begin{cases} t, & 0 \leq t < 1, \\ 2 - t, & 1 \leq t < 2, \\ 0, & \text{其他区间}. \end{cases} $$$B_2(t)$ - 支撑区间[1,3]
$$ B_2(t) = \begin{cases} t - 1, & 1 \leq t < 2, \\ 3 - t, & 2 \leq t < 3, \\ 0, & \text{其他区间}. \end{cases} $$$B_3(t)$ - 支撑区间[2,4]
$$ B_3(t) = \begin{cases} t - 2, & 2 \leq t < 3, \\ 4 - t, & 3 \leq t \leq 4, \\ 0, & \text{其他区间}. \end{cases} $$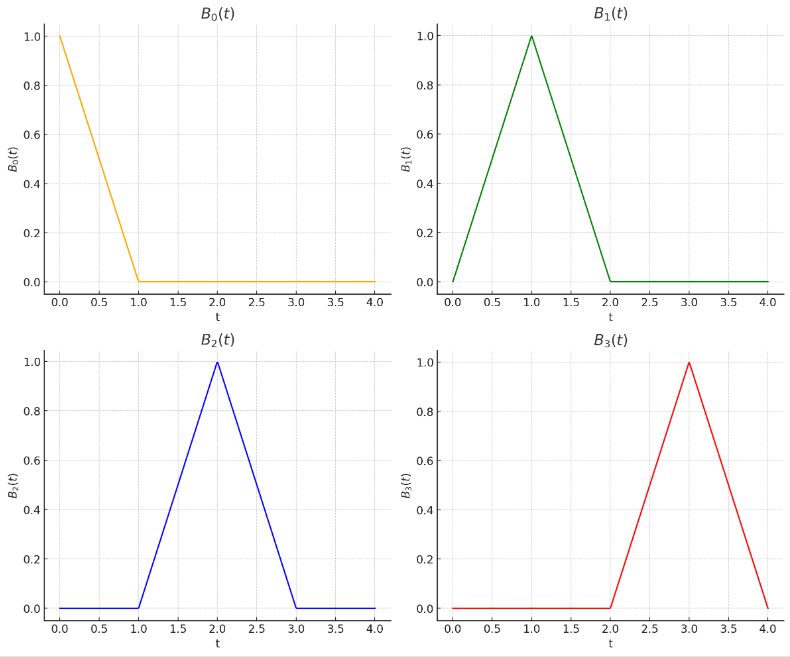
假设用该基函数对$f(t) = \sin\left(\dfrac{\pi t}{4}\right)$在[0,4]区间上拟合
$$ S(t) = 0 \cdot B_0(t) + 0.7071 \cdot B_1(t) + 1 \cdot B_2(t) + 0.7071 \cdot B_3(t) $$
网络结构:
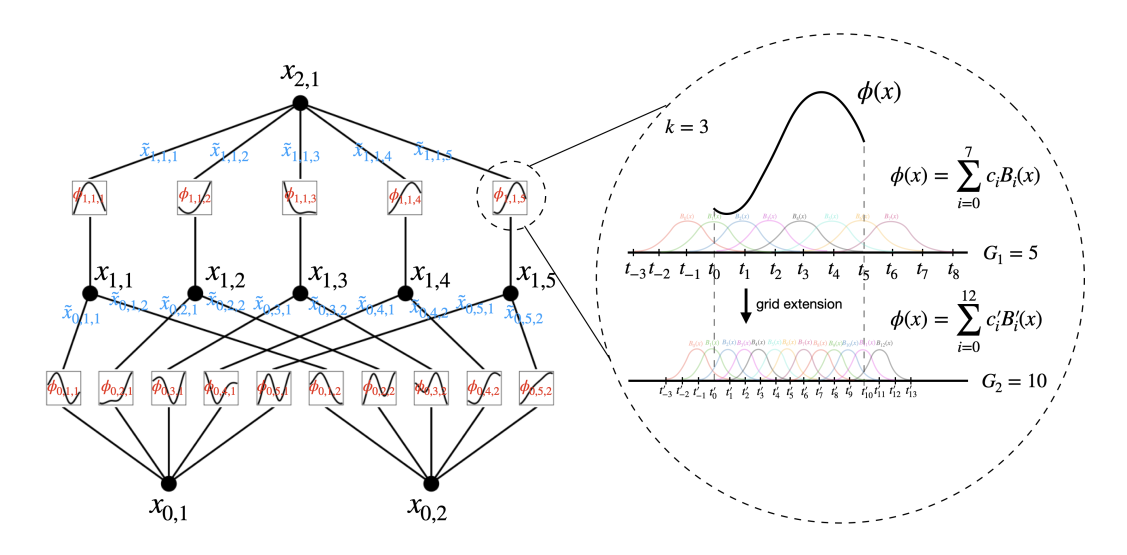
左图:
- 节点(如$x_{l,i}$)表示第$l$层第$i$个神经元的输入值
- 边(如$\phi_{l,j,i}$)表示可学习的激活函数(权重)
- 下一层节点的值计算:
$$x_{l+1,j} = \sum_i \phi_{l,j,i}(x_{l,i})$$
右图:
