力扣Hot 100题

杂项

最大值：Integer.MAX_VALUE
最小值：Integer.MIN_VALUE

数组集合比较

Arrays.equals(array1, array2)

用于比较两个数组是否相等（内容相同）。
支持多种类型的数组（如 int[]、char[]、Object[] 等）。

int[] arr1 = {1, 2, 3};
int[] arr2 = {1, 2, 3};
boolean isEqual = Arrays.equals(arr1, arr2); // true

Collections 类本身没有直接提供类似 Arrays.equals 的方法来比较两个集合的内容是否相等。不过，Java 中的集合类（如 List、Set、Map）已经实现了 equals 方法

List<Integer> list1 = Arrays.asList(1, 2, 3);
        List<Integer> list2 = Arrays.asList(1, 2, 3);
        List<Integer> list3 = Arrays.asList(3, 2, 1);
        System.out.println(list1.equals(list2)); // true
        System.out.println(list1.equals(list3)); // false（顺序不同）

逻辑比较

boolean flag = false;
if (!flag) {    //! 是 Java 中的逻辑非运算符，只能用于对布尔值取反。
    System.out.println("flag 是 false");
}

if (flag == false) {             //更常用！
    System.out.println("flag 是 false");
}
//java中没有 if(not flag) 这种写法！

Character好用的方法

Character.isDigit(char c)用于判断一个字符是否是一个数字字符

Character.isLetter(char c)用于判断字符是否是一个字母（大小写字母都可以）。

Character.isLowerCase(char c)判断字符是否是小写字母。

Character.toLowerCase(char c)将字符转换为小写字母。

Integer好用的方法

Integer.parseInt(String s)：将字符串 s 解析为一个整数（int）。

Integer.toString(int i)：将 int 转换为字符串。

Integer.compare(int a,int b) 比较a和b的大小，内部实现类似：

public static int compare(int x, int y) {
    return (x < y) ? -1 : ((x == y) ? 0 : 1);
}

避免了 整数溢出 的风险，在排序中建议使用Integer.compare(a,b)代替 a-b。注意，仅支持Integer[] arr，不支持int[] arr。

位运算

按位与 &：只有两个对应位都为 1 时，结果位才为 1。

int a = 5;       // 0101₂  
int b = 3;       // 0011₂  
int c = a & b;   // 0001₂ = 1  
System.out.println(c);  // 输出 1

按位或 |: 只要两个对应位有一个为 1，结果位就为 1。

int a = 5;       // 0101₂  
int b = 3;       // 0011₂  
int c = a | b;   // 0111₂ = 7  
System.out.println(c);  // 输出 7

按位异或 ^: 两个对应位不同则为 1，相同则为 0。

int a = 5;       // 0101₂  
int b = 3;       // 0011₂  
int c = a ^ b;   // 0110₂ = 6  
System.out.println(c);  // 输出 6

左移 <<: 整体二进制左移 N 位，右侧补 0；相当于乘以 2ⁿ。

int a = 3;       // 0011₂  
int b = a << 2;  // 1100₂ = 12  
System.out.println(b);  // 输出 12

常用数据结构

String

子串：字符串中连续的一段字符。

子序列：字符串中按顺序选取的一段字符，可以不连续。

异位词：字母相同、字母频率相同、顺序不同，如"listen" 和 "silent"

排序：

需要String先转为char [] 数组，排序好之后再转为String类型！！

char[] charArray = str.toCharArray();
Arrays.sort(charArray);
String sortedStr = new String(charArray);

取字符：

charAt(int index) 方法返回指定索引处的 char 值。
char 是基本数据类型，占用 2 个字节，表示一个 Unicode 字符。
HashSet<Character> set = new HashSet<Character>();

取子串：

substring(int beginIndex, int endIndex) 方法返回从 beginIndex 到 endIndex - 1 的子字符串。
返回的是 String 类型，即使子字符串只有一个字符。

StringBuffer

StringBuffer 是 Java 中用于操作可变字符串的类

public class StringBufferExample {
    public static void main(String[] args) {
        // 创建初始字符串 "Hello"
        StringBuffer sb = new StringBuffer("Hello");
        System.out.println("Initial: " + sb.toString());  // 输出 "Hello"
        
        // 1. append：在末尾追加 " World"
        sb.append(" World");
        System.out.println("After append: " + sb.toString());  // 输出 "Hello World"
        
        // 2. insert：在索引 5 位置（"Hello"后）插入 ", Java"
        sb.insert(5, ", Java");
        System.out.println("After insert: " + sb.toString());  // 输出 "Hello, Java World"
        
        // 3. delete：删除从索引 5 到索引 11（不包含）的子字符串（即删除刚才插入的 ", Java"）
        sb.delete(5, 11);
        //sb.delete(5, sb.length()); 删除到末尾
        System.out.println("After delete: " + sb.toString());  // 输出 "Hello World"
        
        // 4. deleteCharAt：删除索引 5 处的字符（删除空格）
        sb.deleteCharAt(5);
        System.out.println("After deleteCharAt: " + sb.toString());  // 输出 "HelloWorld"
        
        // 5. reverse：反转整个字符串
        sb.reverse();
        System.out.println("After reverse: " + sb.toString());  // 输出 "dlroWolleH"
    }
}

StringBuffer有库函数可以翻转，String未提供！

StringBuilder sb = new StringBuilder(s);
String reversed = sb.reverse().toString();

StringBuffer清空内容：

StringBuffer sb = new StringBuffer("Hello, world!");
System.out.println("Before clearing: " + sb);
// 清空 StringBuffer
sb.setLength(0);

StringBuffer 的 append() 方法不仅支持添加普通的字符串，也可以直接将另一个 StringBuffer 对象添加到当前的 StringBuffer。

HashMap

基于哈希表实现，查找、插入和删除的平均时间复杂度为 O(1)。
不保证元素的顺序。

import java.util.HashMap;
import java.util.Map;

public class HashMapExample {
    public static void main(String[] args) {
        // 创建 HashMap
        Map<String, Integer> map = new HashMap<>();

        // 添加键值对
        map.put("apple", 10);
        map.put("banana", 20);
        map.put("orange", 30);

        // 获取值
        int appleCount = map.get("apple");   //如果获取不存在的元素，返回null
        System.out.println("Apple count: " + appleCount); // 输出 10

        // 遍历 HashMap
        for (Map.Entry<String, Integer> entry : map.entrySet()) {
            System.out.println(entry.getKey() + ": " + entry.getValue());
        }
        // 输出：
        // apple: 10
        // banana: 20
        // orange: 30

        // 检查是否包含某个键
        boolean containsBanana = map.containsKey("banana");
        System.out.println("Contains banana: " + containsBanana); // 输出 true

        // 删除键值对
        map.remove("orange");   //删除不存在的元素也不会报错
        System.out.println("After removal: " + map); // 输出 {apple=10, banana=20}
    }
}

记录二维数组中某元素是否被访问过，推荐使用：

int m = grid.length;
int n = grid[0].length;
boolean[][] visited = new boolean[m][n];

// 访问 (i, j) 时标记为已访问
visited[i][j] = true;

而非创建自定义Pair二元组作为键用Map记录。

HashSet

基于哈希表实现，查找、插入和删除的平均时间复杂度为 O(1)。
不保证元素的顺序!!因此不太用iterator迭代，而是用contains判断是否有xx元素。

  import java.util.HashSet;
  import java.util.Set;
  
  public class HashSetExample {
      public static void main(String[] args) {
          // 创建 HashSet
          Set<Integer> set = new HashSet<>();
  
          // 添加元素
          set.add(10);
          set.add(20);
          set.add(30);
          set.add(10); // 重复元素，不会被添加
  
          // 检查元素是否存在
          boolean contains20 = set.contains(20);
          System.out.println("Contains 20: " + contains20); // 输出 true
  
          // 遍历 HashSet
          for (int num : set) {
              System.out.println(num);
          }
          // 输出：
          // 20
          // 10
          // 30
  
          // 删除元素
          set.remove(20);
          System.out.println("After removal: " + set); // 输出 [10, 30]
      }
  }

PriorityQueue

基于优先堆（最小堆或最大堆）实现，元素按优先级排序。
默认是最小堆，即队首元素是最小的。 new PriorityQueue<>(Comparator.reverseOrder());定义最大堆
支持自定义排序规则，通过 Comparator 实现。

常用方法：

add(E e) / offer(E e)：

功能：将元素插入队列。
时间复杂度：O(log n)
区别
- add：当队列满时会抛出异常。
- offer：当队列满时返回 false，不会抛出异常。

remove() / poll()：

功能：移除并返回队首元素。
时间复杂度：O(log n)
区别
- remove：队列为空时抛出异常。
- poll：队列为空时返回 null。

element() / peek()：

功能：查看队首元素，但不移除。
时间复杂度：O(1)
区别
- element：队列为空时抛出异常。
- peek：队列为空时返回 null。

clear()：

功能：清空队列。
时间复杂度：O(n)（因为需要删除所有元素）

import java.util.PriorityQueue;
import java.util.Comparator;

public class PriorityQueueExample {
    public static void main(String[] args) {
        // 创建 PriorityQueue（默认是最小堆）
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();

        // 添加元素
        minHeap.add(10);
        minHeap.add(20);
        minHeap.add(5);

        // 查看队首元素
        System.out.println("队首元素: " + minHeap.peek()); // 输出 5

        // 遍历 PriorityQueue（注意：遍历顺序不保证有序）
        System.out.println("遍历 PriorityQueue:");
        for (int num : minHeap) {
            System.out.println(num);
        }
        // 输出：
        // 5
        // 10
        // 20

        // 移除队首元素
        System.out.println("移除队首元素: " + minHeap.poll()); // 输出 5

        // 再次查看队首元素
        System.out.println("队首元素: " + minHeap.peek()); // 输出 10

        // 创建最大堆（通过自定义 Comparator）
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
        maxHeap.add(10);
        maxHeap.add(20);
        maxHeap.add(5);

        // 查看队首元素
        System.out.println("最大堆队首元素: " + maxHeap.peek()); // 输出 20

        // 清空队列
        minHeap.clear();
        System.out.println("队列是否为空: " + minHeap.isEmpty()); // 输出 true
    }
}

自定义排序：按第二个元素的值构建小根堆

如何比较器返回负数，则第一个数排在前面->优先级高->在堆顶

public class CustomPriorityQueue {
    public static void main(String[] args) {
        // 定义一个 PriorityQueue，其中每个元素是 int[]，并且按照数组第二个元素升序排列
        PriorityQueue<int[]> minHeap = new PriorityQueue<>(
            (a, b) -> return a[i]-b[i];
        );
        
        // 添加数组
        minHeap.offer(new int[]{1, 2});
        minHeap.offer(new int[]{3, 4});
        minHeap.offer(new int[]{0, 5});
        
        // 依次取出元素，输出结果
        while (!minHeap.isEmpty()) {
            int[] arr = minHeap.poll();
            System.out.println(Arrays.toString(arr));
        }
    }
}

不用lambda版本：

PriorityQueue<int[]> minHeap = new PriorityQueue<>(new Comparator<int[]>() {
    @Override
    public int compare(int[] a, int[] b) {
        return a[1] - b[1];
    }
});

自己实现小根堆：

父节点：对于任意索引 i，其父节点的索引为 (i - 1) // 2。

左子节点：索引为 i 的节点，其左子节点的索引为 2 * i + 1。

右子节点：索引为 i 的节点，其右子节点的索引为 2 * i + 2。

上滤与下滤操作

上滤（Sift-Up）：用于插入操作。将新加入的元素与其父节点不断比较，若小于父节点则交换，直到满足堆序性质。
下滤（Sift-Down）：用于删除操作或建堆。将根节点或某个节点与其子节点中较小的进行比较，若大于子节点则交换，直至满足堆序性质。

建堆：从数组中最后一个非叶节点开始（索引为 heapSize/2 - 1），对每个节点执行下滤操作（sift-down）

插入元素：将新元素插入到堆的末尾，然后执行上滤操作（sift-up），以保持堆序性质。

弹出元素（删除堆顶）：弹出操作一般是删除堆顶元素（小根堆中即最小值），然后用堆尾元素替代堆顶，再进行下滤操作。

class MinHeap {
    private int[] heap; // 数组存储堆元素
    private int size;   // 当前堆中元素的个数

    // 构造函数，初始化堆，capacity为堆的最大容量
    public MinHeap(int capacity) {
        heap = new int[capacity];
        size = 0;
    }

    // 插入元素：先将新元素添加到数组末尾，然后执行上滤操作恢复堆序性质
    public void insert(int value) {
        if (size >= heap.length) {
            throw new RuntimeException("Heap is full");
        }
        // 将新元素放到末尾
        heap[size] = value;
        int i = size;
        size++;

        // 上滤操作：不断与父节点比较，若新元素小于父节点则交换
        while (i > 0) {
            int parent = (i - 1) / 2;
            if (heap[i] < heap[parent]) {
                swap(heap, i, parent);
                i = parent;
            } else {
                break;
            }
        }
    }

    // 弹出堆顶元素：移除堆顶（最小值），用最后一个元素替换堆顶，然后下滤恢复堆序
    public int pop() {
        if (size == 0) {
            throw new RuntimeException("Heap is empty");
        }
        int min = heap[0];
        // 将最后一个元素移到堆顶
        heap[0] = heap[size - 1];
        size--;
        // 对新的堆顶执行下滤操作，恢复堆序性质
        minHeapify(heap, 0, size);
        return min;
    }

    // 建堆：将无序数组a构造成小根堆，heapSize为数组长度
    public static void buildMinHeap(int[] a, int heapSize) {
        for (int i = heapSize / 2 - 1; i >= 0; --i) {
            minHeapify(a, i, heapSize);
        }
    }

    // 下滤操作：从索引i开始，将子树调整为小根堆
    public static void minHeapify(int[] a, int i, int heapSize) {
        int l = 2 * i + 1, r = 2 * i + 2;
        int smallest = i;
        // 判断左子节点是否存在且比当前节点小
        if (l < heapSize && a[l] < a[smallest]) {
            smallest = l;
        }
        // 判断右子节点是否存在且比当前最小节点小
        if (r < heapSize && a[r] < a[smallest]) {
            smallest = r;
        }
        // 如果最小值不是当前节点，交换后继续对被交换的子节点执行下滤操作
        if (smallest != i) {
            swap(a, i, smallest);
            minHeapify(a, smallest, heapSize);
        }
    }

    // 交换数组中两个位置的元素
    public static void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

}

改为大根堆只需要把里面 ''<'' 符号改为 ''>''

ArrayList

基于数组实现，支持动态扩展。
访问元素的时间复杂度为 O(1)，在末尾插入和删除的时间复杂度为 O(1)。
在指定位置插入和删除O(n) add(int index, E element) remove(int index)

复制链表(list set queue都有addAll方法，map是putAll)：

List<Integer> list1 = new ArrayList<>();
// 假设 list1 中已有数据
List<Integer> list2 = new ArrayList<>();
list2.addAll(list1);   //法一
List<Integer> list2 = new ArrayList<>(list1);  //法二

清空(list set map queue map都有clear方法):

List<Integer> list = new ArrayList<>();
// 清空 list
list.clear();

import java.util.ArrayList;
import java.util.List;

public class ArrayListExample {
    public static void main(String[] args) {
        // 创建 ArrayList
        List<Integer> list = new ArrayList<>();

        // 添加元素
        list.add(10);
        list.add(20);
        list.add(30);
        
        int size = list.size(); // 获取列表大小
		System.out.println("Size of list: " + size); // 输出 3

        // 获取元素
        int firstElement = list.get(0);
        System.out.println("First element: " + firstElement); // 输出 10

        // 修改元素
        list.set(1, 25); // 将第二个元素改为 25
        System.out.println("After modification: " + list); // 输出 [10, 25, 30]

        // 遍历 ArrayList
        for (int num : list) {
            System.out.println(num);
        }
        // 输出：
        // 10
        // 25
        // 30

        // 删除元素
        list.remove(2); // 删除第三个元素
        System.out.println("After removal: " + list); // 输出 [10, 25]
    }
}

如果事先不知道嵌套列表的大小如何遍历呢？

import java.util.ArrayList;
import java.util.List;

int rows = 3;
int cols = 3;
List<List<Integer>> list = new ArrayList<>();


for (List<Integer> row : list) {
    for (int num : row) {
        System.out.print(num + " ");
    }
    System.out.println(); // 换行
}
for (int i = 0; i < list.size(); i++) {
    List<Integer> row = list.get(i);
    for (int j = 0; j < row.size(); j++) {
        System.out.print(row.get(j) + " ");
    }
    System.out.println(); // 换行
}

数组（Array）

数组是一种固定长度的数据结构，用于存储相同类型的元素。数组的特点包括：

固定长度：数组的长度在创建时确定，无法动态扩展。
快速访问：通过索引访问元素的时间复杂度为 O(1)。
连续内存：数组的元素在内存中是连续存储的。

public class ArrayExample {
    public static void main(String[] args) {
        // 创建数组
        int[] array = new int[5]; // 创建一个长度为 5 的整型数组

        // 添加元素
        array[0] = 10;
        array[1] = 20;
        array[2] = 30;
        array[3] = 40;
        array[4] = 50;

        // 获取元素
        int firstElement = array[0];
        System.out.println("First element: " + firstElement); // 输出 10

        // 修改元素
        array[1] = 25; // 将第二个元素改为 25
        System.out.println("After modification:");
        for (int num : array) {
            System.out.println(num);
        }
        // 输出：
        // 10
        // 25
        // 30
        // 40
        // 50

        // 遍历数组
        System.out.println("Iterating through array:");
        for (int i = 0; i < array.length; i++) {
            System.out.println("Index " + i + ": " + array[i]);
        }
        // 输出：
        // Index 0: 10
        // Index 1: 25
        // Index 2: 30
        // Index 3: 40
        // Index 4: 50

        // 删除元素（数组长度固定，无法直接删除，可以通过覆盖实现）
        int indexToRemove = 2; // 要删除的元素的索引
        for (int i = indexToRemove; i < array.length - 1; i++) {
            array[i] = array[i + 1]; // 将后面的元素向前移动
        }
        array[array.length - 1] = 0; // 最后一个元素置为 0（或其他默认值）
        System.out.println("After removal:");
        for (int num : array) {
            System.out.println(num);
        }
        // 输出：
        // 10
        // 25
        // 40
        // 50
        // 0

        // 数组长度
        int length = array.length;
        System.out.println("Array length: " + length); // 输出 5
    }
}

复制数组：

int[] source = {1, 2, 3, 4, 5};
int[] destination = Arrays.copyOf(source, source.length);
int[] partialArray = Arrays.copyOfRange(source, 1, 4);   //复制指定元素，不包括索引4

初始化：

int double 数值默认初始化为0，boolean默认初始化为false

int[] memo = new int[nums.length];
Arrays.fill(memo, -1);

二维数组

int rows = 3;
int cols = 3;
int[][] array = new int[rows][cols];
// 填充数据
for (int i = 0; i < rows; i++) {
    for (int j = 0; j < cols; j++) {
        array[i][j] = i * cols + j + 1;
    }
}
//创建并初始化
int[][] array = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

// 遍历二维数组，不知道几行几列
public void setZeroes(int[][] matrix) {
    // 遍历每一行
    for (int i = 0; i < matrix.length; i++) {
        // 遍历当前行的每一列
        for (int j = 0; j < matrix[i].length; j++) {
            // 这里可以处理 matrix[i][j] 的元素
            System.out.print(matrix[i][j] + " ");
        }
        System.out.println(); // 换行，便于输出格式化
    }
}

[[1, 0]] 是一行两列数组。

Queue

队尾插入，队头取！

import java.util.Queue;
import java.util.LinkedList;

public class QueueExample {
    public static void main(String[] args) {
        // 创建一个队列
        Queue<Integer> queue = new LinkedList<>();

        // 添加元素到队列中
        queue.add(10);       // 使用 add() 方法添加元素
        queue.offer(20);     // 使用 offer() 方法添加元素
        queue.add(30);
        System.out.println("队列内容：" + queue);

        // 查看队头元素，不移除
        int head = queue.peek();
        System.out.println("队头元素（peek）： " + head);

        // 移除队头元素
        int removed = queue.poll();
        System.out.println("移除的队头元素（poll）： " + removed);
        System.out.println("队列内容：" + queue);

        // 再次移除队头元素
        int removed2 = queue.remove();
        System.out.println("移除的队头元素（remove）： " + removed2);
        System.out.println("队列内容：" + queue);
    }
}

Deque(双端队列+栈)

支持在队列的两端（头和尾）进行元素的插入和删除。这使得 Deque 既能作为队列（FIFO）又能作为栈（LIFO）使用。

建议在需要栈操作时使用 Deque 的实现

栈

Deque<Integer> stack = new ArrayDeque<>();
//Deque<Integer> stack = new LinkedList<>();
stack.push(1);   // 入栈
Integer top1=stack.peek()
Integer top = stack.pop();   // 出栈

LinkedList 是基于双向链表实现的，每个节点存储数据和指向前后节点的引用。
ArrayDeque 则基于动态数组实现，内部使用循环数组来存储数据。
ArrayDeque 在大多数情况下性能更好，因为数组在内存中连续，缓存友好，且操作（如 push/pop）开销更小。

双端队列

在队头操作

addFirst(E e)：在队头添加元素，如果操作失败会抛出异常。
offerFirst(E e)：在队头插入元素，返回 true 或 false 表示是否成功。
peekFirst()：查看队头元素，不移除；队列为空返回 null。
removeFirst()：移除并返回队头元素；队列为空会抛出异常。
pollFirst()：移除并返回队头元素；队列为空返回 null。

在队尾操作

addLast(E e)：在队尾添加元素，若失败会抛出异常。
offerLast(E e)：在队尾插入元素，返回 true 或 false 表示是否成功。
peekLast()：查看队尾元素，不移除；队列为空返回 null。
removeLast()：移除并返回队尾元素；队列为空会抛出异常。
pollLast()：移除并返回队尾元素；队列为空返回 null。

添加元素：调用 add(e) 或 offer(e) 时，实际上是调用 addLast(e) 或 offerLast(e)，即在队尾添加元素。

删除或查看元素：调用 remove() 或 poll() 时，则是调用 removeFirst() 或 pollFirst()，即在队头移除元素；同理，element() 或 peek() 则是查看队头元素。

import java.util.Deque;
import java.util.LinkedList;

public class DequeExample {
    public static void main(String[] args) {
        // 使用 LinkedList 实现双端队列
        Deque<Integer> deque = new LinkedList<>();

        // 在队列头部添加元素
        deque.addFirst(10);
        // 在队列尾部添加元素
        deque.addLast(20);
        // 在队列头部插入元素
        deque.offerFirst(5);
        // 在队列尾部插入元素
        deque.offerLast(30);

        System.out.println("双端队列内容：" + deque);

        // 查看队头和队尾元素，不移除
        int first = deque.peekFirst();
        int last = deque.peekLast();
        System.out.println("队头元素：" + first);
        System.out.println("队尾元素：" + last);

        // 从队头移除元素
        int removedFirst = deque.removeFirst();
        System.out.println("移除队头元素：" + removedFirst);
        // 从队尾移除元素
        int removedLast = deque.removeLast();
        System.out.println("移除队尾元素：" + removedLast);

        System.out.println("双端队列最终内容：" + deque);
    }
}

Iterator

HashMap、HashSet、ArrayList 和 PriorityQueue 都实现了 Iterable 接口，支持 iterator() 方法。

Iterator 接口中包含以下主要方法：

hasNext()：如果迭代器还有下一个元素，则返回 true，否则返回 false。
next()：返回迭代器的下一个元素，并将迭代器移动到下一个位置。
remove()：从迭代器当前位置删除元素。该方法是可选的，不是所有的迭代器都支持。

import java.util.ArrayList;
import java.util.Iterator;

public class Main {
    public static void main(String[] args) {
        // 创建一个 ArrayList 集合
        ArrayList<Integer> list = new ArrayList<>();
        list.add(1);
        list.add(2);
        list.add(3);

        // 获取集合的迭代器
        Iterator<Integer> iterator = list.iterator();

        // 使用迭代器遍历集合并输出元素
        while (iterator.hasNext()) {
            Integer element = iterator.next();
            System.out.println(element);
        }
    }
}

排序

排序时间复杂度:O(nlog(n))

求最大值：O(n)

快速排序

基本思想：

快速排序是一种基于“分治”思想的排序算法，通过选定一个“枢轴元素（pivot）”，将数组划分为左右两个子区间：左边都小于等于 pivot，右边都大于等于 pivot；然后对这两个子区间递归排序，最终使整个数组有序。

public class QuickSortWithSwap {
    
    // 交换数组中两个元素的位置
    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    private static void quickSort(int[] arr, int low, int high) {
        if (low < high) {
            int pivotPos = partition(arr, low, high); // 划分
            quickSort(arr, low, pivotPos - 1);  // 递归排序左子表
            quickSort(arr, pivotPos + 1, high); // 递归排序右子表
        }
    }

    private static int partition(int[] arr, int low, int high) {
        int pivot = arr[low]; // 选取第一个元素作为枢轴
        int left = low;       // 左指针
        int right = high;     // 右指针
        
        while (left < right) {
            // 从右向左找第一个小于枢轴的元素
            while (left < right && arr[right] >= pivot) {
                right--;
            }
            // 从左向右找第一个大于枢轴的元素
            while (left < right && arr[left] <= pivot) {
                left++;
            }
            // 交换这两个元素
            if (left < right) {
                swap(arr, left, right);
            }
        }
        // 将枢轴放到最终位置
        swap(arr, low, left);
        return left; // 返回枢轴的位置
    }

    public static void main(String[] args) {
        int[] arr = {49, 38, 65, 97, 76, 13, 27, 49};
 
        quickSort(arr, 0, arr.length - 1);
        
        System.out.println("\n排序后:");
        for (int num : arr) {
            System.out.print(num + " ");
        }
    }
}

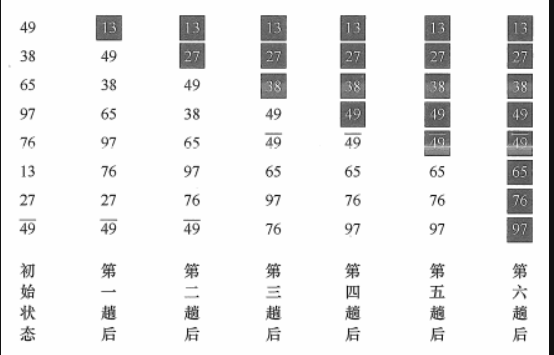
冒泡排序

基本思想：

【每次将最小/大元素，通过依次交换顺序，放到首/尾位。】

从后往前（或从前往后）两两比较相邻元素的值，若为逆序, 则交换它们，直到序列比较完。我们称它为第一趟冒泡，结果是将最小的元素交换到待排序列的第一个位置（或将最大的元素交换到待排序列的最后一个位置）；
下一趟冒泡时，前一趟确定的最小元素不再参与比较，每趟冒泡的结果是把序列中的最小元素（或最大元素）放到了序列的最终位置。
……这样最多做n - 1趟冒泡就能把所有元素排好序。
如若有一趟没有元素交换位置，则可提前说明已排好序。

public void bubbleSort(int[] arr){
        //n-1 趟冒泡
        for (int i = 0; i < arr.length-1; i++) {
            boolean flag=false;
            //冒泡
            for (int j = arr.length-1; j >i ; j--) {
                if (arr[j-1]>arr[j]){
                    swap(arr,j-1,j);
                    flag=true;
                }
            }
            //本趟遍历后没有发生交换，说明表已经有序
            if (!flag){
                return;
            }
        }
    }
    private void swap(int[] arr,int i,int j){
        int temp=arr[i];
        arr[i]=arr[j];
        arr[j]=temp;
    }

归并排序

基本思想：

将待排序的数组视为多个有序子表，每个子表的长度为 1，通过两两归并逐步合并成一个有序数组。

实现思路

分解：递归地将数组拆分成两个子数组，直到每个子数组只有一个元素。
合并：将两个有序子数组合并为一个有序数组。

时间复杂度： O(n log n)，无论最坏、最好、平均情况。

public class MergeSort {

    /**
     * 归并排序（入口函数）
     * @param arr 待排序数组
     */
    public static void mergeSort(int[] arr) {
        if (arr == null || arr.length <= 1) {
            return; // 边界条件
        }
        int[] temp = new int[arr.length]; // 辅助数组
        mergeSort(arr, 0, arr.length - 1, temp);
    }

    private static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (right + left) / 2; 
            mergeSort(arr, left, mid, temp);     // 递归左子数组
            mergeSort(arr, mid + 1, right, temp); // 递归右子数组
            merge(arr, left, mid, right, temp);  // 合并两个有序子数组
        }
    }

    private static void merge(int[] arr, int left, int mid, int right, int[] temp) {
        int i = left;    // 左子数组起始指针
        int j = mid + 1; // 右子数组起始指针
        int t = 0;       // 辅助数组指针

        // 1. 按序合并两个子数组到temp
        while (i <= mid && j <= right) {
            if (arr[i] <= arr[j]) { // 注意等号保证稳定性
                temp[t++] = arr[i++];
            } else {
                temp[t++] = arr[j++];
            }
        }

        // 2. 将剩余元素拷贝到temp
        while (i <= mid) {
            temp[t++] = arr[i++];
        }
        while (j <= right) {
            temp[t++] = arr[j++];
        }

        // 3. 将temp中的数据复制回原数组
        t = 0;
        while (left <= right) {
            arr[left++] = temp[t++];
        }
    }
}

数组排序

默认升序：

import java.util.Arrays;

public class ArraySortExample {
    public static void main(String[] args) {
        int[] numbers = {5, 2, 9, 1, 5, 6};
        Arrays.sort(numbers); // 对数组进行排序
        System.out.println(Arrays.toString(numbers)); // 输出 [1, 2, 5, 5, 6, 9]
    }
}

Arrays.sort(nums, i + 1, n); 等价于把 nums[i+1] 到 nums[n-1] 这段做升序排序。

自定义降序：

注意：如果数组元素是对象（例如 Integer、String 或自定义类）那么可以利用 Arrays.sort() 方法配合自定义的比较器（Comparator）实现降序排序。例如，对于 Integer 数组，可以这样写：

public class DescendingSortExample {
    public static void main(String[] args) {
        // 创建一个Integer数组
        Integer[] arr = {5, 2, 9, 1, 5, 6};

        // 使用Comparator进行降序排序（使用lambda表达式）
        Arrays.sort(arr, (a, b) -> Integer.compare(b, a));
        // 或者使用Collections.reverseOrder()也可以：
        
        // 对下标 [1, 4) 的区间，也就是 {2,9,1}，按降序排序
        Arrays.sort(arr, 1, 4, Collections.reverseOrder());

        // 输出排序后的数组
        System.out.println(Arrays.toString(arr));
    }
}

对于基本数据类型的数组（如 int[]、double[] 等），Arrays.sort() 方法仅支持升序排序，需要先对数组进行升序排序，然后反转数组元素顺序！。

public class DescendingPrimitiveSort {
    public static void main(String[] args) {
        int[] arr = {5, 2, 9, 1, 5, 6};

        // 先排序（升序）
        Arrays.sort(arr);

        // 反转数组
        for (int i = 0; i < arr.length / 2; i++) {
            int temp = arr[i];
            arr[i] = arr[arr.length - 1 - i];
            arr[arr.length - 1 - i] = temp;
        }

        // 输出结果
        System.out.println(Arrays.toString(arr));
    }
}

集合排序

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class ListSortExample {
    public static void main(String[] args) {
        // 创建一个 ArrayList 并添加元素
        List<Integer> numbers = new ArrayList<>();
        numbers.add(5);
        numbers.add(2);
        numbers.add(9);
        numbers.add(1);
        numbers.add(5);
        numbers.add(6);

        // 对 List 进行排序
        Collections.sort(numbers);

        // 输出排序后的 List
        System.out.println(numbers); // 输出 [1, 2, 5, 5, 6, 9]
    }
}

自定义排序

要实现接口自定义排序，必须实现 Comparator<T> 接口的 compare(T o1, T o2) 方法。

Comparator 接口中定义的 compare(T o1, T o2) 方法返回一个整数（非布尔值！！），这个整数的正负意义如下：

如果返回负数，说明 o1 排在 o2前面。
如果返回零，说明 o1 等于 o2。
如果返回正数，说明 o1 排在 o2后面。

自定义比较器排序二维数组 用Lambda表达式实现Comparator<int[]>接口

import java.util.Arrays;

public class IntervalSort {
    public static void main(String[] args) {
        int[][] intervals = { {1, 3}, {2, 6}, {8, 10}, {15, 18} };

        // 自定义比较器，先比较第一个元素，如果相等再比较第二个元素
        Arrays.sort(intervals, (a, b) -> {
            if (a[0] != b[0]) {
                return Integer.compare(a[0], b[0]);
            } else {
                return Integer.compare(a[1], b[1]);
            }
        });

        // 输出排序结果
        for (int[] interval : intervals) {
            System.out.println(Arrays.toString(interval));
        }
    }
}

对象排序，不用lambda方式

import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;

class Person {
    String name;
    int age;

    public Person(String name, int age) {
        this.name = name;
        this.age = age;
    }

    @Override
    public String toString() {
        return name + " (" + age + ")";
    }
}

public class ComparatorSortExample {
    public static void main(String[] args) {
        // 创建一个 Person 列表
        List<Person> people = new ArrayList<>();
        people.add(new Person("Alice", 25));
        people.add(new Person("Bob", 20));
        people.add(new Person("Charlie", 30));

        // 使用 Comparator 按姓名排序,匿名内部类形式
        Collections.sort(people, new Comparator<Person>() {
            @Override
            public int compare(Person p1, Person p2) {
                return p1.name.compareTo(p2.name); // 按姓名升序排序
            }
        });
        
        // 使用 Comparator 按姓名排序，使用 lambda 表达式
        //Collections.sort(people, (p1, p2) -> p1.name.compareTo(p2.name));

        // 输出排序后的列表
        System.out.println(people); // 输出 [Alice (25), Bob (20), Charlie (30)]
    }
}

题型

常见术语：

子串（Substring）：子字符串是字符串中连续的非空字符序列

回文串(Palindrome)：回文串是向前和向后读都相同的字符串。

子序列（(Subsequence)）：可以通过删除原字符串中任意个字符（不改变剩余字符的相对顺序）得到的序列，不要求连续。例如 "abc" 的 "ac" 就是一个子序列。

前缀 (Prefix) ：从字符串起始位置开始的连续字符序列，如 "leetcode" 的前缀 "lee"。

字母异位词 (Anagram)：由相同字符组成但排列顺序不同的字符串。例如 "abc" 与 "cab" 就是异位词。

子集、幂集：数组的子集是从数组中选择一些元素（可能为空）。例如，对于集合 S = {1, 2}，其幂集为： { ∅, {1}, {2}, {1, 2} }，子集有{1}

哈希

问题分析：

确定是否需要快速查找或存储数据。
判断是否需要统计元素频率或检查元素是否存在。

适用场景

快速查找：
- 当需要频繁查找元素时，哈希表可以提供 O(1) 的平均时间复杂度。
统计频率：
- 统计元素出现次数时，哈希表是常用工具。
去重：
- 需要去除重复元素时，HashSet 可以有效实现。

双指针

题型：

同向双指针：两个指针从同一侧开始移动，通常用于滑动窗口或链表问题。
对向双指针：两个指针从两端向中间移动，通常用于有序数组或回文问题。重点是考虑移动哪个指针可能优化结果！！！
快慢指针：两个指针以不同速度移动，通常用于链表中的环检测或中点查找。

适用场景：

有序数组的两数之和：

在对向双指针的帮助下，可以在 O(n) 时间内找到两个数，使它们的和等于目标值。

滑动窗口：

用于解决子数组或子字符串问题，如同向双指针可以在 O(n) 时间内找到满足条件的最短或最长子数组。

链表中的环检测：

快慢指针可以用于检测链表中是否存在环，并找到环的起点。

回文问题：

对向双指针可以用于判断字符串或数组是否是回文。

合并有序数组或链表：

双指针可以用于合并两个有序数组或链表，时间复杂度为 O(n)。

前缀和

前缀和的定义
定义前缀和 preSum[i] 为数组 nums 从索引 0 到 i 的元素和，即
$$ \text{preSum}[i] = \sum_{j=0}^{i} \text{nums}[j] $$
子数组和的关系
对于任意子数组 nums[i+1..j]（其中 0 ≤ i < j < n），其和可以表示为
$$ \text{sum}(i+1,j) = \text{preSum}[j] - \text{preSum}[i] $$ 当这个子数组的和等于 k 时，有
$$ \text{preSum}[j] - \text{preSum}[i] = k $$ 即
$$ \text{preSum}[i] = \text{preSum}[j] - k $$ $\text{preSum}[j] - k$表示 "以当前位置结尾的子数组和为k"
利用哈希表存储前缀和
我们可以使用一个哈希表 prefix 来存储每个前缀和出现的次数。
- 初始时，prefix[0] = 1，表示前缀和为 0 出现一次（对应空前缀）。
- 遍历数组，每计算一个新的前缀和 preSum，就查看 preSum - k 是否在哈希表中。如果存在，则说明之前有一个前缀和等于 preSum - k，那么从该位置后一个位置到当前索引的子数组和为 k，累加其出现的次数。
时间复杂度
该方法只需要遍历数组一次，时间复杂度为 O(n)。

遍历二叉树

递归法中序

public void inOrderTraversal(TreeNode root, List<Integer> list) {
    if (root != null) {
        inOrderTraversal(root.left, list);     // 遍历左子树
        list.add(root.val);                    // 访问当前节点
        inOrderTraversal(root.right, list);    // 遍历右子树
    }
}

迭代法中序

public void inOrderTraversalIterative(TreeNode root, List<Integer> list) {
    Deque<TreeNode> stack = new ArrayDeque<>();
    TreeNode curr = root;

    while (curr != null || !stack.isEmpty()) {
        // 一路向左入栈
        while (curr != null) {
            stack.push(curr);  // push = addFirst
            curr = curr.left;
        }

        // 弹出栈顶并访问
        curr = stack.pop();     // pop = removeFirst
        list.add(curr.val);

        // 转向右子树
        curr = curr.right;
    }
}

迭代法前序

public void preOrderTraversalIterative(TreeNode root, List<Integer> list) {
    if (root == null) return;

    Deque<TreeNode> stack = new ArrayDeque<>();
    stack.push(root);

    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        list.add(node.val); // 先访问当前节点

        // 注意：先压右子节点，再压左子节点
        // 因为栈是“后进先出”的，先弹出的是左子节点
        if (node.right != null) {
            stack.push(node.right);
        }
        if (node.left != null) {
            stack.push(node.left);
        }
    }
}

层序遍历BFS

public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        if (root == null) return result;
        
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            int levelSize = queue.size();
            List<Integer> level = new ArrayList<>();
            
            for (int i = 0; i < levelSize; i++) {
                TreeNode node = queue.poll();
                level.add(node.val);
                
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            result.add(level);
        }
        
        return result;
    }

回溯法

回溯算法用于 搜索一个问题的所有的解 ，即爆搜（暴力解法），通过深度优先遍历的思想实现。核心思想是：

1.逐步构建解答：

回溯算法通过逐步构造候选解，当构造的部分解满足条件时继续扩展；如果发现当前解不符合要求，则“回溯”到上一步，尝试其他可能性。

2.剪枝（Pruning）：

在构造候选解的过程中，算法会判断当前部分解是否有可能扩展成最终的有效解。如果判断出无论如何扩展都不可能得到正确解，就立即停止继续扩展该分支，从而节省计算资源。

3.递归调用

回溯通常通过递归来实现。递归函数在每一层都尝试不同的选择，并在尝试失败或达到终点时返回上一层重新尝试其他选择。

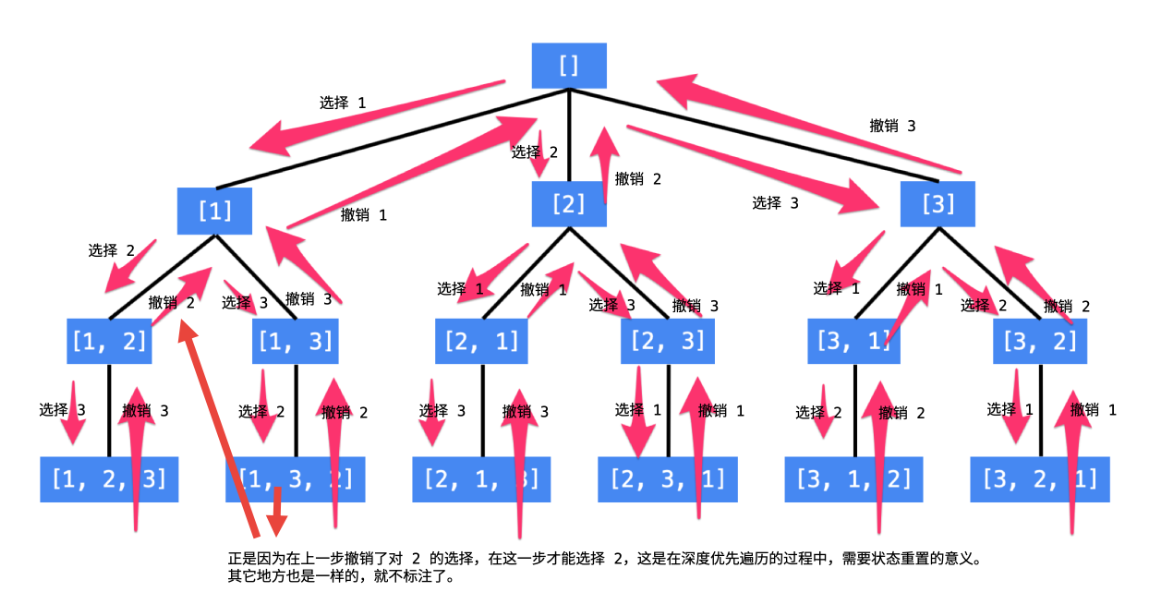
例：以数组 [1, 2, 3] 的全排列为例。

先写以 1 开头的全排列，它们是：[1, 2, 3], [1, 3, 2]，即 1 + [2, 3] 的全排列（注意：递归结构体现在这里）；再写以 2 开头的全排列，它们是：[2, 1, 3], [2, 3, 1]，即 2 + [1, 3] 的全排列；最后写以 3 开头的全排列，它们是：[3, 1, 2], [3, 2, 1]，即 3 + [1, 2] 的全排列。

public class Permute {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        // 用来标记数组中数字是否被使用
        boolean[] used = new boolean[nums.length];
        List<Integer> path = new ArrayList<>();
        backtrack(nums, used, path, res);
        return res;
    }

    private void backtrack(int[] nums, boolean[] used, List<Integer> path, List<List<Integer>> res) {
        // 当path中元素个数等于nums数组的长度时，说明已构造出一个排列
        if (path.size() == nums.length) {
            res.add(new ArrayList<>(path));
            return;
        }
        // 遍历数组中的每个数字
        for (int i = 0; i < nums.length; i++) {
            // 如果该数字已经在当前排列中使用过，则跳过
            if (used[i]) {
                continue;
            }
            // 选择数字nums[i]
            used[i] = true;
            path.add(nums[i]);
            // 递归构造剩余的排列
            backtrack(nums, used, path, res);
            // 回溯：撤销选择，尝试其他数字
            path.remove(path.size() - 1);
            used[i] = false;
        }
    }
}

大小根堆

题目描述：给定一个整数数组 nums 和一个整数 k，返回出现频率最高的前 k 个元素，返回顺序可以任意。

解法一：大根堆（最大堆）

思路：

使用 HashMap 统计每个元素的出现频率。
构建一个大根堆（PriorityQueue + 自定义比较器），根据频率降序排列。
将所有元素加入堆中，弹出前 k 个元素即为答案。

适合场景：

实现简单，适用于对全部元素排序后取前 k 个。
时间复杂度：O(n log n)，因为需要将所有 n 个元素都加入堆。

解法二：小根堆（最小堆）

思路：

使用 HashMap 统计频率。
构建一个小根堆，堆中仅保存前 k 个高频元素。
遍历每个元素：
- 如果堆未满，直接加入。
- 如果当前元素频率大于堆顶（最小频率），则弹出堆顶，加入当前元素。
最终堆中保存的就是前 k 个高频元素。

方法	适合场景	时间复杂度	空间复杂度
大根堆	k ≈ n，简单易写	O(n log n)	O(n)
小根堆	k ≪ n，更高效	O(n log k)	O(n)

动态规划

解题步骤：

确定 dp 数组以及下标的含义（很关键！不跑偏）

目的：明确 dp 数组中存储的状态或结果。
关键：下标往往对应问题中的一个“阶段”或“子问题”，而数组的值则表示这一阶段的最优解或累计结果。
示例：在背包问题中，可以设 dp[i] 表示前 i 个物品能够达到的最大价值。

确定递推公式

目的：找到状态之间的转移关系，表明如何从已解决的子问题求解更大规模的问题。
关键：分析每个状态可能来源于哪些小状态，写出数学或逻辑表达式。
示例：对于 0-1 背包问题，递推公式通常为 $$ dp[i]=max⁡(dp[i],dp[i−weight]+value) $$

dp 数组如何初始化

目的：给定初始状态，为所有可能情况设置基础值。
关键：通常初始化基础的情况（如 dp[0]=0），或者用极大或极小值标示未计算状态。
示例：在求最短路径问题中，可以用较大值（如 infinity）初始化所有状态，然后设定起点状态为 0。

确定遍历顺序

目的：按照正确的顺序计算每个状态，确保依赖的子问题都已经计算完毕。
关键：遍历顺序需要与递推公式保持一致，既可以是正向（从小到大）也可以是反向（从大到小），取决于问题要求。
示例：对背包问题，为避免重复计算，每个物品的更新通常采用反向遍历。

举例推导 dp 数组

目的：通过一个具体例子来演示递推公式的应用，直观理解每一步计算。
关键：选择简单案例，从初始化、更新到最终结果展示整个过程。
示例：对一个简单的路径问题，展示如何从起点逐步更新 dp 数组，最后得到终点的最优解。

例题

题目： 746. 使用最小花费爬楼梯 (MinCostClimbingStairs)
描述：给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。

示例 2：输入：cost = [10,15,20] 输出：15 解释：你将从下标为 1 的台阶开始。

支付 15 ，向上爬两个台阶，到达楼梯顶部。总花费为 15 。

链接：https://leetcode.cn/problems/min-cost-climbing-stairs/

1.确定dp数组以及下标的含义

dp[i]的定义：到达第i台阶所花费的最少体力为dp[i]。

2.确定递推公式

可以有两个途径得到dp[i]，一个是dp[i-1] 一个是dp[i-2]。

dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。

dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。

那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢？

一定是选最小的，所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);

3.dp数组如何初始化

看一下递归公式，dp[i]由dp[i - 1]，dp[i - 2]推出，既然初始化所有的dp[i]是不可能的，那么只初始化dp[0]和dp[1]就够了，其他的最终都是dp[0]、dp[1]推出。

由“你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” =》初始化 dp[0] = 0，dp[1] = 0

4.确定遍历顺序

因为是模拟台阶，而且dp[i]由dp[i-1]dp[i-2]推出，所以是从前到后遍历cost数组就可以了。

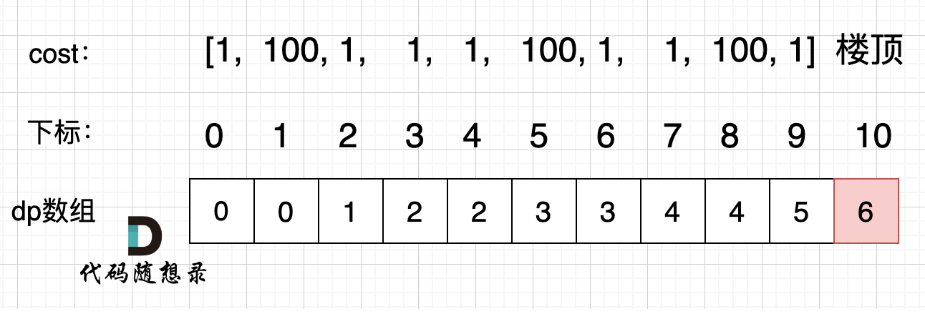
5.举例推导dp数组

拿示例：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ，来模拟一下dp数组的状态变化，如下：

背包问题

总结：背包问题不仅可以求能装的物品的最大价值，还可以求背包是否可以装满，还可以求组合总和。

背包是否可以装满示例说明

假设背包容量为 10，物品的重量分别为 [3, 4, 7]。我们希望判断是否可以恰好填满容量 10。

其中 dp[j] 表示在容量 j 下，能装入的最大重量（保证不超过 j）。如果dp[10]=10，代表能装满

public boolean canFillBackpack(int[] weights, int capacity) {
        // dp[j] 表示在不超过背包容量 j 的前提下，能装入的最大重量
        int[] dp = new int[capacity + 1];
        // 初始状态: 背包容量为0时，能够装入的重量为0，其他位置初始为0
        
        // 遍历每一个物品（0/1背包，每个物品只能使用一次）
        for (int i = 0; i < weights.length; i++) {
            // 逆序遍历背包容量，防止当前物品被重复使用
            for (int j = capacity; j >= weights[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - weights[i]] + weights[i]);
            }
        }
        
        // 如果 dp[capacity] 恰好等于 capacity，则说明背包正好被装满
        return dp[capacity] == capacity;
    }

求组合总和

统计数组中有多少种组合（子集）使得其和正好为 P ？

dp[j] 表示从数组中选取若干个数，使得这些数的和正好为 j 的方法数。

状态转移：对于数组中的每个数字 numnumnum，从 dp 数组后向前（逆序）遍历，更新：

dp[j]=dp[j]+dp[j−num]

这里的意思是：

如果不选当前数字，方法数保持不变；
如果选当前数字，那么原来凑出和 j−num 的方案都可以扩展成凑出和 j 的方案。

初始条件：

dp[0] = 1，代表凑出和为 0 只有一种方式，即不选任何数字。

代码随想录

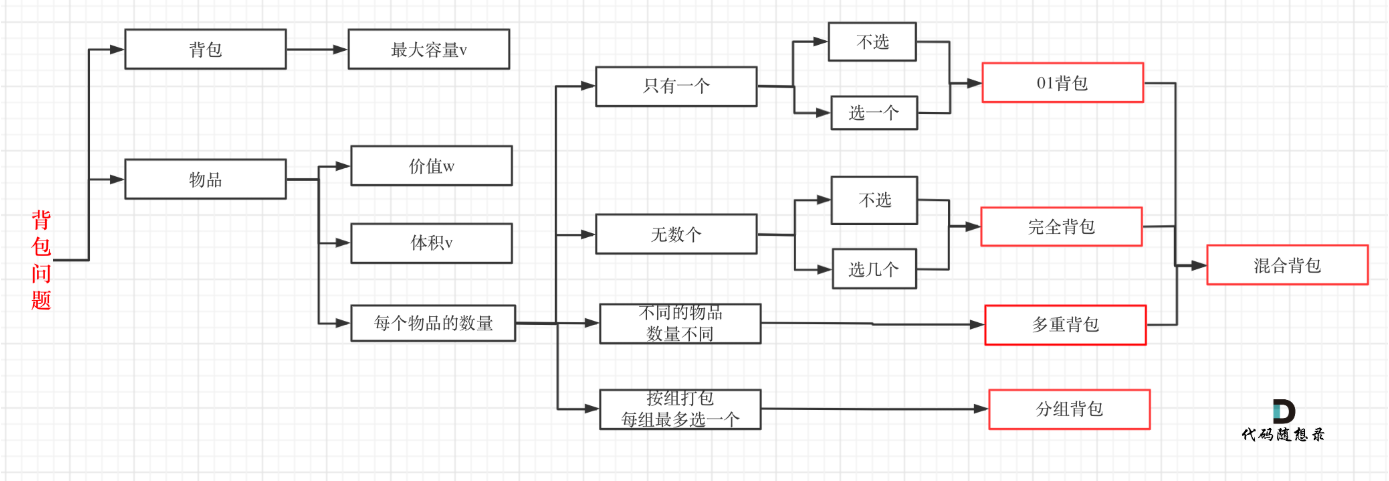
完全背包是01背包稍作变化而来，即：完全背包的物品数量是无限的。

0/1背包（一）

描述：有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

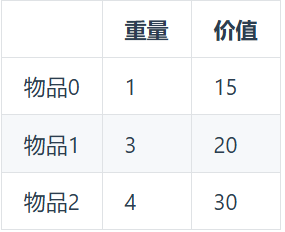
1.确定dp数组以及下标的含义

因为有两个维度需要分别表示：物品和背包容量，所以 dp为二维数组。

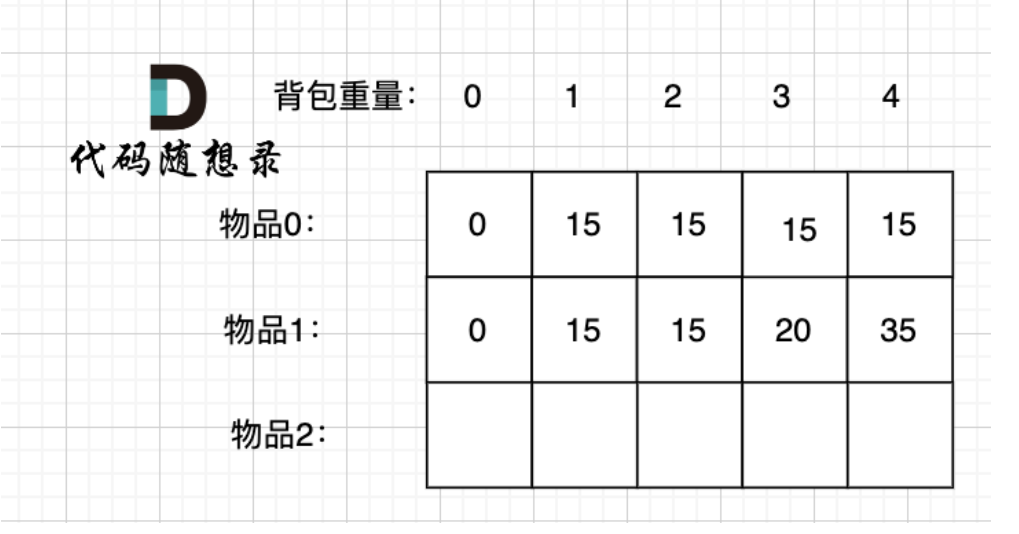
即 dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

2. 确定递推公式

考虑dp[i][j]，有两种情况：

不放物品i：背包容量为j，里面不放物品i的最大价值是 dp[i - 1][j]。
放物品i：背包空出物品i的容量后，背包容量为 j - weight[i]，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

3. dp数组如何初始化

（1）首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。

（2）由状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。

此时就看存放编号0的物品的时候，各个容量的背包所能存放的最大价值。

（3）其他地方初始化为0

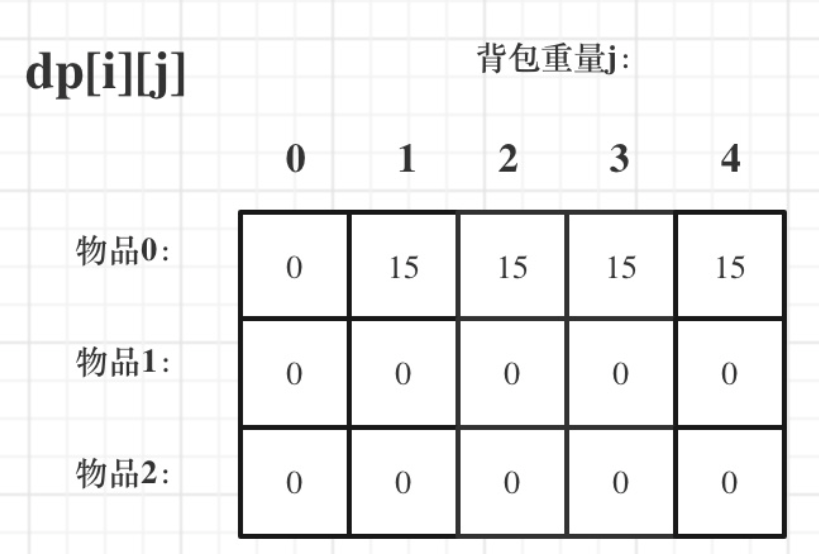
4.确定遍历顺序

都可以，但推荐先遍历物品

// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

    }
}

5.举例推导dp数组

略

代码：

 public int knapsack(int[] weight, int[] value, int capacity) {
        int n = weight.length; // 物品的总个数
        
        // 定义二维 dp 数组：
        // dp[i][j] 表示从下标为 [0, i] 的物品中任意选择，放入容量为 j 的背包中，能够获得的最大价值
        int[][] dp = new int[n][capacity + 1];
        
        // 1. 初始化第 0 行：只考虑第 0 个物品的情况
        // 当背包容量 j >= weight[0] 时，可以选择放入第 0 个物品，价值为 value[0]；否则为 0
        for (int j = 0; j <= capacity; j++) {
            if (j >= weight[0]) {
                dp[0][j] = value[0];
            } else {
                dp[0][j] = 0;
            }
        }
        
        // 2. 状态转移：从第 1 个物品开始，逐步填表
        // 遍历物品，物品下标从 1 到 n-1
        for (int i = 1; i < n; i++) {
            // 遍历背包容量，从 0 到 capacity
            for (int j = 0; j <= capacity; j++) {
                // 情况一：不放第 i 个物品，则最大价值不变，继承上一行的值
                dp[i][j] = dp[i - 1][j];
                
                // 情况二：如果当前背包容量 j 大于等于物品 i 的重量，则考虑放入当前物品
                if (j >= weight[i]) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - weight[i]] + value[i]);
                }
            }
        }
        
        // 返回考虑所有物品，背包容量为 capacity 时的最大价值
        return dp[n - 1][capacity];
    }

0/1背包（二）

可以将二维 dp 优化为一维 dp 的典型条件包括：

1.状态转移只依赖于之前的状态（例如上一行或上一个层次），而不是当前行中动态更新的状态。

例如在 0/1 背包问题中，二维 dp[i][j] 只依赖于 dp[i-1][j] 和 dp[i-1][j - weight[i]]。

2.存在确定的遍历顺序（例如逆序或正序）能够确保在更新一维 dp 时，所依赖的值不会被当前更新覆盖。

逆序遍历：例如 0/1 背包问题，为了防止同一个物品被重复使用，需要对容量 j 从大到小遍历，确保 dp[j - weight] 的值还是上一轮（上一行）的。
正序遍历：在一些问题中，如果状态更新不会导致当前状态被重复利用（例如完全背包问题），可以顺序遍历。

3.状态数足够简单，不需要记录多维信息，仅一个维度的状态即可准确表示和转移问题状态。

1.确定 dp 数组以及下标的含义

使用一维 dp 数组 dp[j] 表示「在当前考虑的物品下，背包容量为 j 时能够获得的最大价值」。

2.确定递推公式 当考虑当前物品 i（重量为 weight[i]，价值为 value[i]）时，有两种选择：

不选当前物品 i： 此时的最大价值为 dp[j]（即前面的状态没有变化）。
选当前物品 i： 当背包容量至少为 weight[i] 时，如果选择物品 i，剩余容量变为 j - weight[i]，则最大价值为 dp[j - weight[i]] 加上 value[i]。

因此，状态转移方程为：

$$ dp[j]=max⁡(dp[j], dp[j−weight[i]]+value[i]) $$ **3.dp 数组如何初始化**

dp[0] = 0，表示当背包容量为 0 时，能获得的最大价值自然为 0。

对于其他容量 dp[j]，初始值也设为 0，dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。确保值不被初始值覆盖即可。

4.一维dp数组遍历顺序

外层遍历物品：从第一个物品到最后一个物品，依次做决策。

内层遍历背包容量（逆序遍历）：遍历容量从 capacity 到当前物品的重量，进行状态更新。

逆序遍历的目的在于确保当前物品在更新过程中只会被使用一次，因为 dp[j - weight[i]] 代表的是上一轮（当前物品未使用前）的状态，不会被当前物品更新后的状态覆盖。

假设物品 $w=2$, $v=3$，背包容量 $C=5$。

错误的正序遍历（$j=2 \to 5$）

$j=2$:
$dp[2] = \max(0, dp[0]+3) = 3$
$\Rightarrow dp = [0, 0, 3, 0, 0, 0]$
$j=4$:
$dp[4] = \max(0, dp[2]+3) = 6$
$\Rightarrow$ 错误：物品被重复使用两次！

5.举例推导dp数组

略

代码：

public int knapsack(int[] weight, int[] value, int capacity) {
        int n = weight.length;
        // 定义 dp 数组，dp[j] 表示背包容量为 j 时的最大价值
        int[] dp = new int[capacity + 1];

        // 初始化：所有 dp[j] 初始为0，dp[0] = 0（无须显式赋值）

        // 外层：遍历每一个物品
        for (int i = 0; i < n; i++) {
            // 内层：逆序遍历背包容量，保证每个物品只被选择一次
            for (int j = capacity; j >= weight[i]; j--) {
                // 更新状态：选择不放入或者放入当前物品后的最大价值
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
            }
        }
        
        // 返回背包总容量为 capacity 时获得的最大价值
        return dp[capacity];
    }

完全背包(一)

完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

例：背包最大重量为4，物品为：

物品	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

1. 确定dp数组以及下标的含义

dp[i][j] 表示从下标为[0-i]的物品，每个物品可以取无限次，放进容量为j的背包，价值总和最大是多少。

2. 确定递推公式

不放物品i：背包容量为j，里面不放物品i的最大价值是dp[i - 1][j]。
放物品i：背包空出物品i的容量后，背包容量为j - weight[i]，dp[i][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值，那么dp[i][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

递推公式： dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);

01背包中是 dp[i - 1][j - weight[i]] + value[i])

因为在完全背包中，物品是可以放无限个，所以即使空出物品1空间重量，那背包中也可能还有物品1，所以此时我们依然考虑放物品0 和物品1 的最大价值即： dp[1][1]，而不是 dp[0][1]。而0/1背包中，既然空出物品1，那背包中也不会再有物品1，即dp[0][1]。

for (int i = 1; i < n; i++) {
            for (int j = 0; j <= capacity; j++) {
                // 不选物品 i，价值不变
                dp[i][j] = dp[i - 1][j];
                // 如果当前背包容量 j 能放下物品 i，则考虑选取物品 i（完全背包内层循环正序或逆序都可以，但这里通常建议正序）
                if (j >= weight[i]) {
                    // 注意：这里选取物品 i 后仍然可以继续选取物品 i，
                    // 所以状态转移方程为 dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])
                    dp[i][j] = Math.max(dp[i][j], dp[i][j - weight[i]] + value[i]);
                }
            }
        }

3. dp数组如何初始化

如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。
由递推公式，有一个方向 i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。即：存放编号0的物品的时候，各个容量的背包所能存放的最大价值。

for (int j = 0; j <= capacity; j++) {
            // 当 j 小于第 0 个物品重量时，无法选取，所以价值为 0
            if (j < weight[0]) {
                dp[0][j] = 0;
            } else {
                // 完全背包允许多次使用物品 0，所以递归地累加
                dp[0][j] = dp[0][j - weight[0]] + value[0];
            }
}

4. 确定遍历顺序

先物品或先背包容量都可，但推荐先物品。

完全背包（二）

压缩成一维dp数组，也就是将上一层拷贝到当前层。

将上一层dp[i-1] 的那一层拷贝到当前层 dp[i] ，那么递推公式由 dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]) 变成： dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i])

压缩成一维，即dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

根据题型选择先遍历物品或者背包，如果求组合数就是外层for循环遍历物品，内层for遍历背包。如果求排列数就是外层for遍历背包，内层for循环遍历物品。 组合不强调元素之间的顺序，排列强调元素之间的顺序。
内层循环正序，不要逆序！因为要利用已经更新的dp数组，允许同一物品重复使用！

注意，完全背包和0/1背包的一维dp形式的递推公式一样，但是遍历顺序不同！！

多重背包

有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量，且价值总和最大。

	重量	价值	数量
物品0	1	15	2
物品1	3	20	3
物品2	4	30	2

把每种物品按数量展开，就转化为0/1背包问题了！相当于物品0-a 物品0-b 物品1-a ....，每个只能用一次。

public int multipleKnapsack(int V, int[] weight, int[] value, int[] count) {
    // 将每件物品按数量展开成 0/1 背包的多个物品
    List<Integer> wList = new ArrayList<>();
    List<Integer> vList = new ArrayList<>();
    for (int i = 0; i < weight.length; i++) {
        for (int k = 0; k < count[i]; k++) {
            wList.add(weight[i]);
            vList.add(value[i]);
        }
    }
    // 0/1 背包 DP
    int[] dp = new int[V + 1];
    int N = wList.size();
    for (int i = 0; i < N; i++) {
        int wi = wList.get(i);
        int vi = vList.get(i);
        for (int j = V; j >= wi; j--) {
            dp[j] = Math.max(dp[j], dp[j - wi] + vi);
        }
    }
    return dp[V];
}